等比数列求和公式 等比数列的概念及公式
2021-03-28 16:13:35文/李傲等比数列和等差数列作为高中的两大基本数列,在数列的学习中占有很重要的地位。下文是等比数列的定义及求和公式,大家可以参考一下。

等比数列求和公式
q≠1时 Sn=a1(1-q^n)/(1-q)=(a1-anq)/(1-q)
q=1时Sn=na1
(a1为首项,an为第n项,d为公差,q 为等比)
这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),等比数列a1≠0。注:q=1时,{an}为常数列。利用等比数列求和公式可以快速的计算出该数列的和。
等比数列的概念
1、等比数列的定义:
一般地,如果一个数列从第二项起,每一项与它的前一项的比都等于一个常数(不为0),那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用q来表示。
定义可以用公式表达为:a(n+1)/an=q(式中n为正整数,q为常数)。特别注意的是,q是一个与项数n无关的常数
2、等比中项:
三个数 a、G、b依次组成等比数列,则G叫做的等比中项,且G2=a+b(等比中项的平方等于前项与后项之积)。
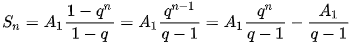 等比数列的性质 什么是等比数列
等比数列的性质 什么是等比数列等比数列的性质是什么?什么是等比数列?小编整理了相...
2021-03-28 无穷等比数列求和公式
无穷等比数列求和公式数列,a,aq,aq^2……aq^n。我们把|q|...
2020-12-10 等比数列前n项和的公式
等比数列前n项和的公式等比数列公式就是在数学上求一定数量的等比数列的和的...
2020-11-10 等比数列前n项和的公式是什么
等比数列前n项和的公式是什么等比数列是非常重要的数学概念,下面小编为大家总结整...
2020-11-24 等比数列求和公式是什么
等比数列求和公式是什么如果一个数列从第2项起,每一项与它的前一项的比等于...
2020-03-30 等比数列性质
等比数列性质等比数列性质:在等比数列{an}{an}中,若m+...
2019-12-10 等比数列怎么求和
等比数列怎么求和在数学中解决问题,通常公式是很重要的一部分,记住公...
2019-12-04 等比数列公式及推导
等比数列公式及推导等比数列公式就是在数学上求一定数量的等比数列的和的...
2019-12-01 等比数列求和公式
等比数列求和公式q≠1时,Sn=a1(1-q^n)/(1-q)=(...
2020-12-17 魔方最后一层通用公式 魔方公式是什么
魔方最后一层通用公式 魔方公式是什么魔方最后一层通用公式是右逆、上顺、右逆、上逆、右逆...
2021-03-28 私立学校和公立学校有什么区别 怎样选择学校
私立学校和公立学校有什么区别 怎样选择学校学校有公立学校和私立学校之分,那么二者到底有哪些区...
2021-03-28 全国一卷的省份 有哪些省
全国一卷的省份 有哪些省全国一卷的省份有哪些?小编整理了相关内容,来看看吧...
2021-03-28 山东省大学排名前十位 山东有哪些高校
山东省大学排名前十位 山东有哪些高校想要报考山东省的小伙伴们,下文是山东省大学排名情况...
2021-03-28 二本最低的医科大学 有哪些学校
二本最低的医科大学 有哪些学校一般来说,好的医学专业的分数都不算低,那么有没有分...
2021-03-28 山河无恙什么意思 有哪些例句
山河无恙什么意思 有哪些例句山河无恙什么意思?有哪些例句?小编整理了相关内容,...
2021-03-28
点击查看 高中数学公式 更多内容





